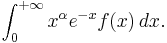Gauss–Laguerre quadrature
In numerical analysis Gauss–Laguerre quadrature is an extension of Gaussian quadrature method for approximating the value of integrals of the following kind:
In this case
where xi is the i-th root of Laguerre polynomial Ln(x) and the weight wi is given by [1]
Contents |
For more general functions
To integrate the function 
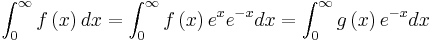 .
.
Generalized Gauss–Laguerre quadrature
More generally, one can also consider integrands that have a known 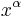 power-law singularity at x=0, for some real number
power-law singularity at x=0, for some real number 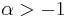 , leading to integrals of the form:
, leading to integrals of the form:
This allows one to efficiently evaluate such integrals for polynomial or smooth f(x) even when α is not an integer.[2]
Program to Calculate Modified Gauss-Laguerre Abscissa And Weights
In Mathematica 7
Suppose want to calculate for n=5
n=5; t = Array[N[Root[LaguerreL[n, x], #]] &, n] w = t/((n + 1)*LaguerreL[(n + 1), t])^2 modW = Array[(Exp[t#]*t#)/(((n + 1)*LaguerreL[(n + 1), t#])^2) &, n]
t is an Abscissa array. w is the corresponding array of weights and modW is the corresponding array of modified weights.
References
- ^ Abramowitz, M & Stegun, I A, Handbook of Mathematical Functions, 10th printing with corrections (1972), Dover, ISBN 978-0-486-61272-0. Equation 25.4.45.access online
- ^ Philip Rabinowitz and George Weiss, "Tables of Abscissas and Weights for Numerical Evaluation of Integrals of the form
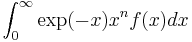 ", Mathematical Tables and Other Aids to Computation, vol. 13, pp. 285–294 (1959).
", Mathematical Tables and Other Aids to Computation, vol. 13, pp. 285–294 (1959).
External Links
- Matlab routine for Gauss–Laguerre quadrature
- generalized Gauss–Laguerre quadrature, free software in Matlab, C++, and Fortran.
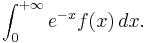
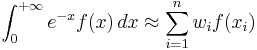
![w_i = \frac {x_i} {(n%2B1)^2[L_{n%2B1}(x_i)]^2}.](/2012-wikipedia_en_all_nopic_01_2012/I/455a95ecbc71004b0c8e503d39a74c86.png)